Teknik Analisis Data Ragam Jenis Uji Normalitas dalam Asumsi Klasik

Uji normalitas merupakan salah satu jenis teknik analisis data dalam uji asumsi klasik. Uji ini juga merupakan salah satu penentu kualitas data yang baik sebelum masuk ke dalam teknik analisis data selanjutnya. Ketika peneliti sudah memutuskan untuk melakukan uji normalitas maka bisa dipastikan peneliti mengikuti teknik analisis data statistik parametrik. 

Analisis statistik parametrik merupakan analisis statistik yang mengasumsikan bahwa distribusi data yang kita gunakan mengikuti suatu distribusi tertentu. Contoh ketika peneliti melakukan uji normalitas maka acuannya adalah tabel distribusi normal. 

Syarat dalam melakukan uji normalitas adalah data harus terdistribusi normal. Maksudnya terdistribusi normal disini adalah data yang memiliki pola distribusi berbentuk lonceng dan simetris. Apabila terdapat indikasi tidak normal alias tidak memenuhi syarat normalitas pada data maka terdapat alternatif lainnya yang bisa diikuti peneliti. 

Misalnya ketika hasilnya tidak terdistribusi normal maka peneliti bisa langsung switch ke analisis statistik non-parametrik. Dimana pada analisis ini, peneliti tidak mengikuti acuan tertentu dalam mengikuti pengujian. Dalam melakukan uji normalitas, ada beberapa cara yang bisa dilakukan oleh sahabat data DQLab sesuai dengan kebutuhan penelitian kamu. 

Cara ini merupakan cara yang paling umum digunakan. Apa sajakah itu? Biar lebih paham, kita simak penjelasannya yuk sahabat DQLab!

1. Kapan Kita Melakukan Uji Normalitas

Banyak peneliti berasumsi bahwa jika banyaknya data sampel sudah memenuhi syarat analisis kuantitatif (dengan n=30) maka data tersebut sudah dikatakan terdistribusi normal. Padahal belum dilakukan pengujian normalitas peneliti pun sudah menduga.

Terkadang sampel yang telah mencapai ratusan pun juga berpeluang untuk mendapatkan sebaran yang tidak berdistribusi normal. Maka ketika kalian sudah memutuskan untuk melakukan uji normalitas maka lakukan. 

Meskipun sampel yang digunakan dalam penelitian kalian ukurannya sudah mencapai 30 atau lebih tetap lakukan uji normalitas. Jika diketahui bahwa dari pengujian normalitas ternyata data yang kita gunakan berdistribusi normal, maka kita seharusnya menggunakan analisis statistik parametrik dan tidak beralih ke analisis statistik nonparametrik. Hal ini karena analisis statistik parametrik lebih powerful dibandingkan analisis nonparametrik. 

Baca juga: Teknik Analisis Data Deskriptif Kualitatif pada Fenomenologi

2. Uji Normalitas Shapiro-Wilk

Uji kedua dalam melakukan pengujian normalitas adalah uji normalitas Shapiro-Wilk. Metode ini sangat efektif dilakukan untuk sampel yang jumlahnya kecil.

Dalam penerapannya, peneliti dapat menggunakan aplikasi statistik yaitu SPSS dan STATA. Uji Shapiro Wilks digunakan untuk mengidentifikasi apakah suatu peubah acak mengikuti distribusi normal. 

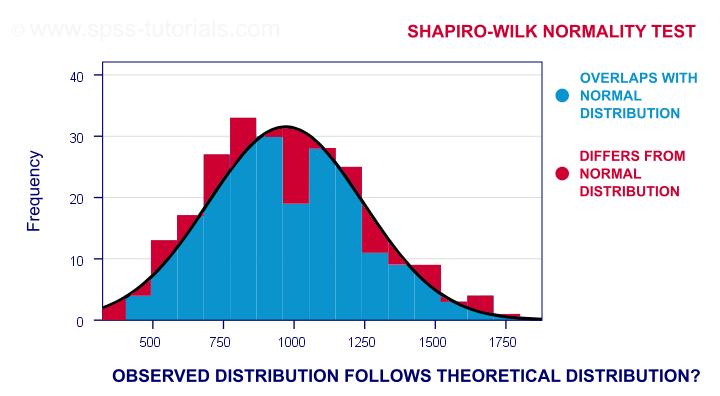
Uji ini sering diaplikasikan dalam analisis regresi untuk pemeriksaan asumsi normalitas. Uji Shapiro Wilks digunakan untuk mengidentifikasi apakah suatu peubah acak (random variable) berdistribusi normal atau tidak.

Shapiro-Wilk memiliki perbedaan dengan uji normalitas Kolmogorov-Smirnov. Kolmogorov-Smirnov digunakan untuk menguji normalitas pada sampel yang jumlahnya banyak (>100), sementara Shapiro-Wilk untuk sampel yang jumlahnya sedikit (<100).

3. Uji Normalitas Lilliefors

Uji ketiga yang bisa menjadi pilihan peneliti untuk melakukan uji normalitas adalah uji Lilliefors. Uji ini dilakukan untuk mengetahui apakah data terdistribusi normal atau tidak pada data tunggal. Uji Normalitas data dengan Liliefors hampir sama dengan menggunakan uji Kolmogorov Smirnov, hanya saja pada uji Liliefors digunakan tabel Liliefors.

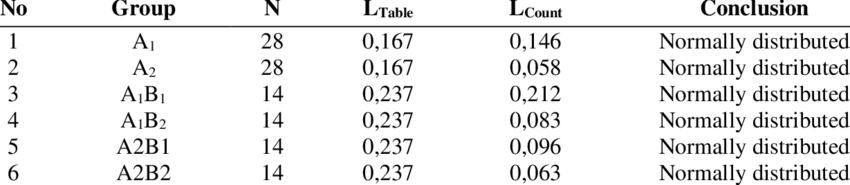
Berikut adalah langkah-langkah untuk melakukan uji normalitas melalui uji Lilliefors:

• Susun data secara berurutan dari skor terkecil sampai skor terbesar

• Hitung rata-rata dan standar deviasi

• Hitung nilai standar baku dengan menggunakan z-score dari masing-masing data

• Tentukan nilai normal standar baku (z-skor) dengan menggunakan tabel normal standar (baku) dari 0 - z

• Tentukan peluang F(zi)

• Tentukan nilai S(zi) dengan cara menghitung porporsi z1, z2,...zn yang lebih kecil atau sama dengan zi dengan rumus:

• Hitung selisih harga mutlak F(zi) “ S(zi)

• Ambil harga mutlak terbesar diantara harga mutlak tersebut dengan symbol Lo (Lilliefors Observasi

• Tentukan nilai L table dengan menggunakan table liliefors (Ltabel (0,05a),(n)) dengan kriteria pembilang  α = 0,05 dan penyebut = n

Bandingkan Lo dengan Ltabel dengan kriteria sebagai berikut:

• Jika Lo lebih besar dari Ltabel berarti populasi berdistribusi tidak normal

• Jika Lo lebih kecil dari Ltabel berarti populasi berdistribusi normal

4. Uji Normalitas Kolmogorov Smirnov

Uji normalitas selanjutnya adalah Uji Kolmogorov-Smirnov yang biasanya dipakai oleh peneliti saat melakukan running data di SPSS.

Uji Kolmogorov Smirnov satu sampel merupakan uji goodness of fit, dimana uji ini berkaitan dengan tingkat kesesuaian antara distribusi sampel (skor observasi) dan distribusi teoritisnya. Uji KS menentukan apakah skor dalam sampel berasal dari populasi yang memiliki distribusi teoritis. 

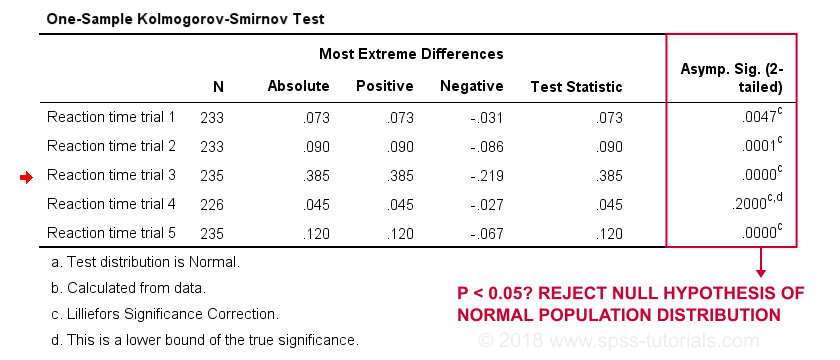
Uji Kolmogorov Smirnov (Chakravart, Laha, dan Roy, 1967) biasa digunakan untuk memutuskan jika sampel berasal dari populasi dengan distribusi spesifik/tertentu. Uji ini membandingkan serangkaian data pada sampel terhadap distribusi normal serangkaian nilai dengan mean dan standar deviasi yang sama.

Singkatnya uji ini dilakukan untuk mengetahui kenormalan distribusi beberapa data. Uji Kolmogorov Smirnov merupakan uji yang lebih kuat daripada uji chi-square ketika asumsi-asumsinya terpenuhi.

5. Uji Normalitas Jarque-Bera

Uji normalitas yang terakhir ialah Uji Normalitas Jarque-Bera. Uji ini merupakan salah satu uji goodness of fit yang digunakan untuk mengukur apakah skewness dan kurtosis sesuai dengan distribusi normal.

Uji ini didasarkan pada kenyataan bahwa nilai skewness, kurtosis dari distribusi normal sama dengan nol. Oleh karena itu, nilai absolute dari parameter ini bisa menjadi ukuran penyimpangan distribusi normal. 

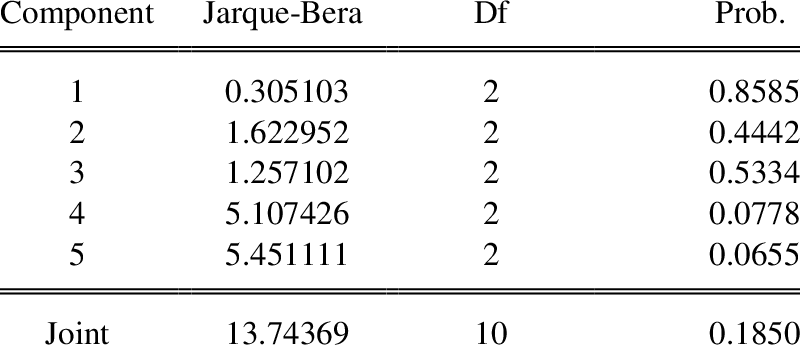
Pengujian menggunakan statistik Jarque-Bera dengan hipotesis sebagai berikut:

H0  : sampel berdistribusi normal, 

H1 : sampel tidak berdistribusi normal. 

Uji Jarque-Bera mempunyai distribusi chi-kuadrat dengan derajat bebas dua. Jika hasil Jarque-Bera lebih besar dari distribusi chi-kuadrat maka ditolak yang berarti tidak berdistribusi normal dan jika sebaliknya maka berarti berdistribusi normal

Baca juga : Langkah-Langkah Menggunakan Teknik Analisis Data Kualitatif

Bagi peneliti pemula, mengenal teknik analisis data merupakan hal yang sulit. Belajar analisis data merupakan salah satu langkah untuk mempelajari hal apapun di ranah data. Melakukan analisis data tentunya bukan hal yang mudah.

Dibutuhkan ketekunan dan ketelitian dalam melakukan setiap tahapannya. Agar skill analisis data kamu semakin terasah, tidak salah lagi jika kamu bisa upgrade skillmu dengan signup di DQLab! Banyak benefit yang bisa kamu dapatkan jika kamu bergabung untuk belajar bersama DQLab! 

Penulis: Reyvan Maulid